De l'excentricité et des trajectoires des planètes

 

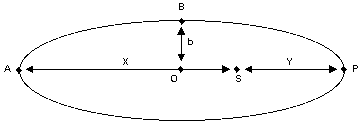
O : centre de l’ellipse
S : le soleil, occupe l’un des foyers de l’ellipse
A : l’aphélie, point de l’orbite où la distance au soleil est la plus grande
P : le périhélie, point de l’orbite où la distance au soleil est la plus petite

On notera SA = X, SP = Y. Les grandeurs OA et OB sont respectivement le demi grand axe et le demi petit axe de l’ellipse. L’excentricité e est le rapport entre la distance du centre O au foyer S et le demi grand axe OA.

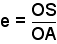
Pour exprimer l’excentricité en fonction de la distance au soleil à l’aphélie et au périhélie, on écrit :

OS = X - OA    et    OA = Y + OS     soit     X + Y = 2 OA    et    X - Y = 2 OS,   d’où :

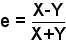Pour connaître la distance moyenne de la planète au soleil, il faut déterminer le rayon R d’une orbite circulaire dont l’aire balayée serait celle de l’orbite elliptique réelle :

Pr² = P ab,   avec a = OA et b = OB

Une ellipse a la propriété suivante : b² = a² (1 - e²).   D’où :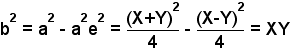


on en déduit donc :

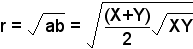C'est pas beau, tout ça ?